Microconical Structure Formation and Field Emission From Atomically Heterogeneous Surfaces Created by Microwave Plasma–Based Low-Energy Ion Beams

We report the formation of self-organized microconical arrays on copper surface when exposed to high flux (5.4 $\times$ 10¹⁵ cm⁻² s⁻¹) of 2 keV argon ion beams at normal incidence. The created microconical arrays are explored for field emission properties. The surface morphologies are investigated by scanning electron microscopy and atomic force microscopy. The local work function variation is analyzed by Kelvin probe force microscopy, and the argon content in the irradiated layer is measured with X-ray Photoelectron Spectroscopy. The average aspect ratio (base width/height) of microstructures for individual irradiated samples is found to increase from 0.7 to 1.5 with a decrease in ion fluence. The ion concentration is highest (3.89 $\text{\%}$) for a fluence of 4.7 $\times$ 10¹⁸ cm⁻², which asserts the formation of atomically heterogeneous surface due to subsurface ion implantation. An enhancement in the field emission properties of the argon ion–treated copper substrates at a fluence of 4.7 $\times$ 10¹⁸ cm⁻² with a low turn-on voltage of 2.33 kV and with electron emission current 0.5 nA has been observed. From the Fowler–Nordheim equations, the field enhancement factor is calculated to be 5,561 for pristine copper, which gets enhanced by a factor of 2–8 times for irradiated substrates. A parametric model is considered, by taking into account the modified local work function caused due to structural undulations of the microstructures and presence of implanted argon ions, for explaining the experimental results on the field enhancement factor and emission current.

1 Introduction

Physical texturing on material surface by bombardment of energetic ion species is a contamination-free and controlled technique of generating micro- or nanostructures of required geometry, composition, and concentration [1–3]. There are extensive experimental reports on growth of variety of self-organized patterns like fuzz, craters, dots, and ripples on carbon nanotubes, graphene sheets, and metallic compounds like ZnO, semiconductors like Si and Ge, and high-Z metals like W, Mo, and Ta, including Pd when irradiated with inert gas ions such as He and Ar [4–7]. The effective surface area gets enhanced due to the production of surface patterns, which in turn act as naturally selected micro- or nanofield electron emitters. Electron emitters with high current density and low turn-on field is desirable for their practical applications in cold electron sources like field emission cathodes (vacuum electronic devices), flat panel displays, gas sensors, magnetic storage devices, and microwave amplifiers including catalytic reactors [8–12]. The apex shape, size, distribution, and the local work function variation of emitters contribute to modify the field emission parameters. Hence, to improve field emission several methods like increasing carrier concentration by ion doping [13], modifying the structures by plasma treatment [14, 15], or creating modified structures by ion bombardment [16] are employed. There are some reports that suggest deposition of metallic impurity atoms of low sputter yield during ion bombardment of metals, leading to the formation of disordered arrays of conical protrusions known as sputter cones [17–19]. On the other hand, in a wide range of devices involving metal surfaces exposed to high electric fields like in plasma facing components of fusion reactors and particle accelerators, field emission current leads to initiation of catastrophic vacuum breakdown (dark current) [20]. Hence, various fundamental studies are carried out to understand the intrinsic mechanism of electron emission under such a high applied field in metallic substrates [21, 22]. Apart from topographical modifications, the surface also becomes heterogeneous in atomic length scale due to the introduction of irradiated ions in the interstitial layers (nm) [23]. The development of surface structures with compositional heterogeneities at the atomic level because of ion irradiation is an important field of research in material processing and thin film studies because of the controllability in the field emission properties that it can offer. The electrical, surface, and optical properties of such atomically heterogeneous metallic systems with patterned arrays of micro- or nanometric dimensions produced by irradiation of high fluence of energetic inert ions have been investigated earlier [23–25].

The present study focuses on the formation of naturally selected metallic field emission arrays. These microprotruding arrays are advantageous for rudimentary studies on various aspects of field emission since generation of electrons (leading to high emission current) is easier because of their low resistivity, high refractivity, and thermal effects [26, 27]. Copper being an earth-abundant element with similar electronic configuration (${\sigma }_{Cu}$ = 5.96 $\times$ 10⁷ Sm⁻¹ at 20°C) of inert metals like gold and silver is considered for generating microstructures by low-energy inert gas ion beam. These modified copper substrates have variety of applications as sensing materials, in aeronautical industries, and as photocatalytic materials [28–30]. However, fundamental field emission experimental studies on such structurally modified plasma ion–irradiated copper substrate have remained unexplored.

In this article, the mechanism of formation of self-organized structures by low-energy ion irradiation and their structural contribution toward enhancement of emission current is explored. The conical structural growths on copper substrate in the absence of secondary metallic impurities are comparatively new and their electron emission response to strong electric fields has not been reported previously. This work presents feasibility of creation of microconical arrays at normal incidence. The experiment of irradiating samples for growth formation is carried over a wide range of fluences. Thereafter, from selectively chosen irradiated substrates, the field emission experiment is carried out individually on the samples.

2 Discussion on Existing Theories on Ion-Irradiated Structure Formation and Field Emission Studies

A variety of theoretical models describe the growth phenomena as competitive processes between orientation-dependent surface diffusion process and sputtering. The Ehrlich–Schwoebel model describes that surface roughening is initiated by temperature-sensitive surface diffusion of adatoms in convex curvatures [31]. The nanoscale bubbles below the material surface coalesce to form craters and nanofibrils near the surface, which to some extent are explained by the surface adatom diffusion model by Martynenko and Nagel [32]. The Bradley–Harper surface instability theory [33] (or some extensions of this theory [34]) explains ripple formation (seen prominently on ion irradiated Si substrate) using the concept of preferential sputtering of concave surfaces with deposition on convex surfaces, especially for irradiation at an angle. The conical protrusions with impurity metal atom resting at the apex of the cones are believed to be formed on the surface to shield the underlying surface from incoming flux [35, 36]. Robinson and Rossnagel’s thermal diffusion model considers the formation and redeposition of impurity clusters as a result of thermal surface diffusion leading to migration of atoms in a random walk pattern [37]. Davidovitch et al. showed that the mass distribution along with erosive surface effects changes the surface height to a considerable degree [38]. Bradley tried to improve upon these models by considering early time dynamics of the initially planar solid surface seeded with impurities during ionic bombardment [39]. Perkinson’s crater function theory incorporates both erosion and mass redistribution effects, neglecting the effects of local curvature at high incidence angles [40].

In the present experiment, no external impurities with differential sputtering yield strength are added. To understand the conical protrusion formation, we consider that at the impact point there is a volumetric removal of material and subsequent deposition after rearrangement, leading to the agglomeration of substrate atoms acting as seeding agents to aid in the growth process. Moreover, the theory for sputter cone formation in the nucleation and growth regime is highly complex and nonlinear and requires profound experimental evidence in order to properly correlate various conditions of the growth pattern formation with varying ion beam parameters and is beyond the scope of this study.

The field emission process (or Fowler–Nordheim tunneling) is quantum tunneling of electrons through electron rich surface–vacuum interface in the presence of a high electric field ($>$1 GV/m). The Fowler–Nordheim (FN) equation assumes a smooth planar metal surface with a given work function, free-electron model (Sommerfeld), and a semi-classical approximation (WKB) for the tunneling probability. The current density J from the Fowler–Nordheim equation is given by the following equation [41, 42]:

$J=\frac{A{\left(\beta E\right)}^2}{{\varphi }^{\frac{3}{2}}}exp\left(-\frac{B{\varphi }^{\frac{3}{2}}}{E\beta }\right),(1)$

where E is the applied electric field, ϕ is the bulk work function, A and B are constants, and A = 1.54 $\times$ 10⁻⁶ AV⁻² eV, and B = 6.83 $\times$ 10⁷ V cm⁻¹ eV^−3/2. The field enhancement factor (β) is a morphology and work function–dependent parameter, affecting the local field around micro (nano)-scale protrusions on the metal surface. As seen from the FN equation (Eq. 1), the field emission current depends on ϕ and β which in turn depends on the aspect ratio and added ion impurities which can modify the work function locally.

The curvature correction on field emitter tips has been recently studied in order to incorporate radius of curvature as an important parameter on which the field enhancement depends upon, reported independently by Kyritsakis and Biswas [43, 44]. Their theoretical results are found to be consistent for tips having radius of curvature within 5–10 nm. The Fowler–Nordheim formula has been modified by considering the local spherical approximation of emitter surface, considering the effect on the image potential due to interactive electrons at a certain distance from the emitter [45]. Density functional theory (DFT) calculations by Djurabekova, Ruzibaev et. al., on copper (100) surface have shown a significant effect on the work function due to microstructures [46]. An ab initio computational method has been developed to calculate the field-emitted current from defective metal surfaces by combining the density functional theory and electronic structure calculations with quantum transport methods on copper (111) surface by Toijala [47]. However, from this model, it is difficult to justify the effective high value of the field enhancement factor in the field emission characteristics of a metal surface, as observed in their as well as our present experiments.

3 Experimental Details

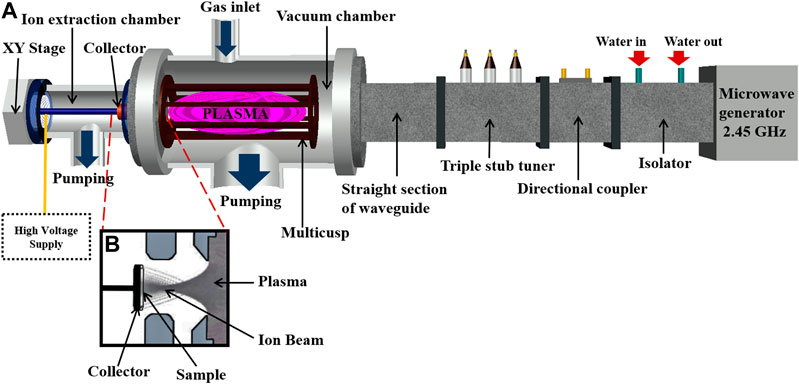
The experimental set-up, shown in Figure 1, comprises of two regions the plasma production chamber and the ion extraction chamber. Microwaves of 2.45 GHz are launched from a magnetron (Alter–TMA20) connected with its power supply and controller (Richardson PM 740). The waves are passed through a metallic rectangular waveguide (WR 340) and a quartz window into the plasma chamber, and the power is maintained at 180 W for continuous mode of operation. A water-cooled isolator (ISO) protects the magnetron from the reflected power. The directional coupler (DC) measures the forward and reflected power of the microwaves. The triple stub tuner (TST) is used for matching the impedance of the magnetron to the plasma, so that maximum power can be transferred to the plasma. The plasma production region consists of a vacuum chamber (VC) of length 50 cm and diameter 20 cm and a magnetic multicusp (octupole) which is placed inside the VC for confinement of the plasma [24]. The ports in the VC are used for gas inlet, probe diagnostics, pressure gages, and venting. The amount of Ar gas entering VC is controlled by a mass flow controller (MKS1179A). The base pressure of VC is kept around $\sim$ 1.33 $\times$ 10⁻⁶ mbar using a turbomolecular pump (Varian 301 Navigator) and a rotary pump, while the working pressure is kept at $\sim$ 1.33 $\times$ 10⁻⁴ mbar. In the ion extraction region, ion beams are extracted from the microwave-induced plasma by employing metallic electrodes. The plasma electrode (PLE), which is the electrode that faces the plasma, is held at the ground potential and has a small aperture diameter of 1 cm. The collector plate on which samples are mounted is floated to a negative high voltage (for the extraction of ions from the plasma) through a vacuum electrical feed-through. At the other end, the collector is attached to an XY stage manipulator. The curved potential lines which bend through the PLE aperture and penetrate into the plasma sheath region act as a lens for the beams and help them focus onto the substrate held on the collector plate [48]. All ions arrive at the PLE with Bohm velocity and have energy $\left(e{V}_p\right)$ corresponding to the difference between the plasma potential (few tens of volts) and the ground potential. From the PLE, they are extracted with the potential applied at the collector ($V_c\sim$ kV). Therefore, all ions are expected to be more or less monoenergetic (e$V_p$ ≪ e$V_c$), as the extraction is made through vacuum and there are no ion-neutral collisions.

FIGURE 1

FIGURE 1. (A) Schematic diagram of experimental setup (not to scale); (B) ion extraction region.

The samples are copper sheets (purity $>$ 99.99 $\text{\%}$ ) of dimensions $1\times 1\times 0.44\mathrm{c}{\mathrm{m}}^{\mathrm{3}}$. In order to remove the hydroxide layer, the substrates are immersed in a prepared solution of 2MOL/l HNO₃ for 45 s and then ultrasonically cleaned by acetone and ethanol. The samples are inserted in an ion extraction chamber and are exposed to energetic argon ions (2 keV) with a flux of 5.431 $\times$ 10¹⁵ cm⁻² s⁻¹ at normal incidence angle (as shown in the inset image of Figure 1). It has been found in earlier works that singly charged ions are dominant in the plasma [49]. Experiments on surface modification is carried out at fluences of 1.3 $\times$ 10¹⁸ cm⁻²— 4.7 $\times$ 10¹⁸ cm⁻². The percentage error on the determined fluence, especially when using plasma to generate the ion beam, is calculated to be $\sim$ 4.2$\text{\%}$. The beam diameter is kept at 1 cm to maintain a uniform irradiation of the exposed part of the sample [23]. The samples after irradiation are kept in vacuum desiccators to prevent any environmental contamination.

The surface morphologies of pristine and irradiated samples are investigated by Zeiss scanning electron microscopy (SEM, Model-SUPRA40VP). Atomic force microscopy (AFM, Model-ASYELEC-01, Asylum Research) provides the evidence of change in surface roughness due to microstructure formation. The MFP: 3D classic atomic force microscopy (AFM) measurements are performed in air with n-type silicon cantilever coated with Ti-Ir. AFM and Kelvin probe force microscopy (KPFM) scans an area of 25 μm² at different locations on the samples to account for all types of irregularities. The KPFM provides the local work function of the surface scanned.

X-ray photoelectron spectroscopy (XPS, Model-5000 Versa Probe II spectrometer, FEI Inc.) technique is employed for elemental analysis. The X-ray beam diameter is 200 μm and the average area over which the sample is probed is 1 mm². The achieved energy resolution is $\text{Δ}$E $\le$ 0.5 eV for Al K_α excitation (1486.6 eV) in ultrahigh vacuum (10⁻⁹ mbar). XPS spectra are calibrated using the reference energy value of carbon core level E (C_1s) = 284.8 eV. The implanted argon concentration ($\text{\%}$) up to second decimal place is calculated from the survey spectral XPS analysis of the peaks using the Casa XPS software.

The digital picture and schematic diagram of the field emission setup is shown in Figure 2. The experiments are performed on both pristine and irradiated samples with developed microcones, at room temperature. The experiments and measurements which are performed at room temperature implied that no additional heating of the substrate is done externally. The substrate is copper, which is a good conductor and the heat generated gets transported away by conduction through the metallic rod handle and radiation. Moreover, we have also performed the experiment by breaking down the time period of irradiation in slots of four for 60 s each and still have observed no significant change in pattern formation. So, we have taken into account the fluence variation as the key factor in generating dense structures. The field emission experimental setup is a parallel plate configuration with gap distance of 2 mm, kept in high vacuum chamber having a base pressure of 1.33 $\times$ 10⁻⁶ mbar. The anode is mirror-polished copper and the cathode is the substrate. The digital picture is the end section of a high vacuum–focused ion beam system, which is employed for the field emission measurements [50].

FIGURE 2

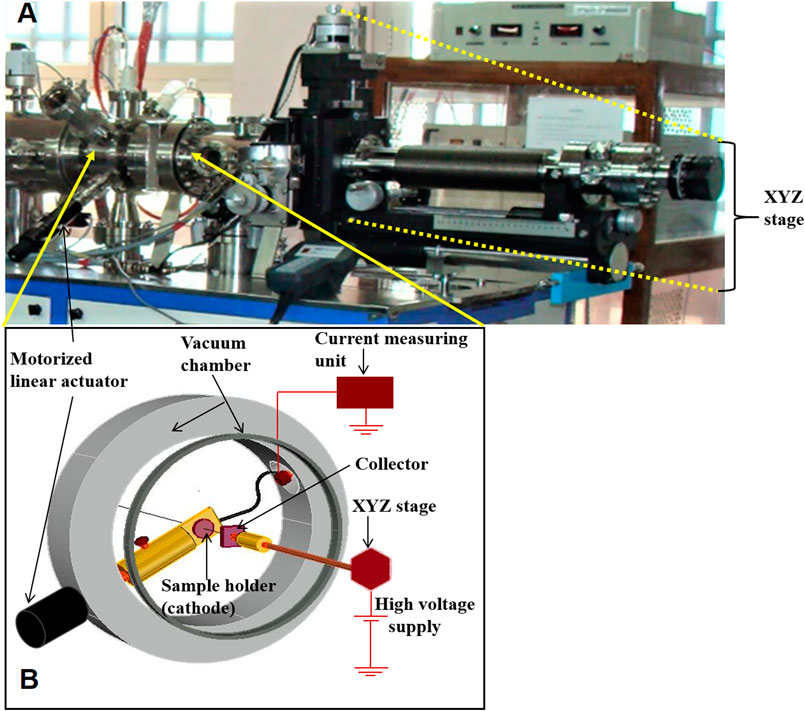
FIGURE 2. (A) Digital picture of experimental setup for field emission measurement experiment (not to scale); (B) the corresponding schematic diagram.

4 Experimental Results and Discussions

Figure 3 shows evenly distributed microstructures as observed from SEM analysis. In Figure 3A, we can see pristine copper with minute bright spots. The contrasting bright spots are initial random roughness generated due to HNO₃ etching to remove the copper hydroxide layer which acts as a precursor of nucleation sites for stabilizing the growth process. Copper substrate exhibits high electrical conductivity, thermal conductivity, malleability, and ductility, which aids in easier structure formation for comparative analysis of field emission effects for a chosen range of fluences, when exposed to high electric field. In Figure 3B at a fluence of 1.3 $\times$ 10¹⁸ cm⁻², the structures are mound-like with well-defined rim. During ion bombardment, the surface gets destabilized by implanted ionic impurities for certain critical impurity flux leading to a microscale mound formation. It is observed from Figure 3C that the mound boundary becomes well defined with the onset of conical tip formation on such individual structures. From Figure 3D to Figure 3F, we see well-defined micro hillocks formation with individual base boundaries and certain protrusion height. It is observed that, with the increase in fluence, the structures become uniformly distributed with a prominent conical shape formation. At the maximum fluence of 4.7 $\times$ 10¹⁸ cm⁻², as seen in Figure 3F, we observe production of self-organized microcones which are densely distributed. The conical mounds slowly become prominent hillocks with increase in ion beam fluence. The protrusion height variation is between 2 and 4 μm having a relatively constant base width of $\sim$ 3 μm. For fluences higher than 5 $\times$ 10¹⁸ cm⁻², the sharpness of these structures reduces with deformation of the peaks. At higher fluences, sputtering erodes away these structures depending upon the strength of the ion beam and tenure of exposure [51]. Thus, optimization of fluences is required as it increases the number of emitters per unit area due to the production of multiple nucleation sites.

FIGURE 3

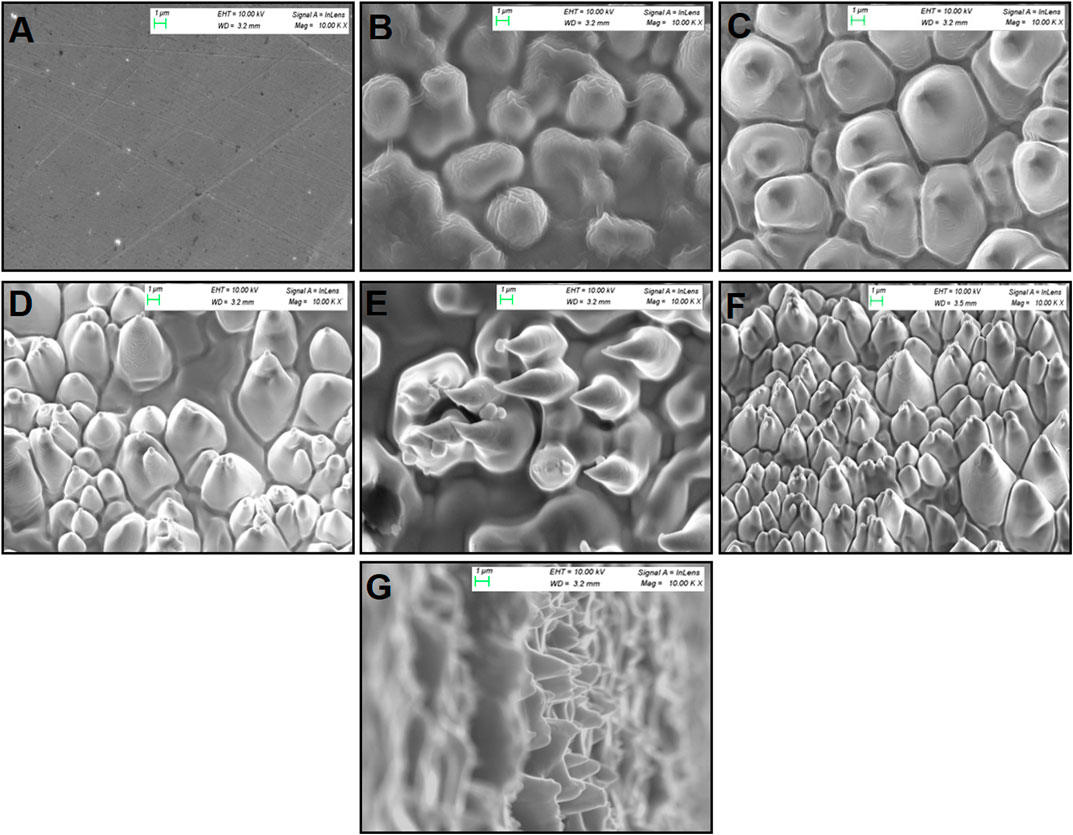
FIGURE 3. SEM images (10 μm $\times$ 10 μm scan area) of (A) pristine Cu sheet, 2 keV Ar⁺ bombarded Cu sheet at normal incidence with fluence; (B) 1.3 $\times$ 10¹⁸ cm⁻², (C) 2.7 $\times$ 10¹⁸ cm⁻², (D) 3.2 $\times$ 10¹⁸ cm⁻², (E) 3.9 $\times$ 10¹⁸ cm⁻², (F) 4.7 $\times$ 10¹⁸ cm⁻², and (G) cross-sectional SEM at 4.7 $\times$ 10¹⁸ cm⁻².

In Figure 4, the AFM and KPFM results are reported. The surface roughness variation of pristine and two of the exposed substrates at fluences of 3.2 $\times$ 10¹⁸ cm⁻² and 4.7 $\times$ 10¹⁸ cm⁻², respectively, are shown. Their corresponding work function distribution with respect to the local surrounding is obtained from KPFM analysis. In Figure 4, as one moves from left to right, the variation in surface topography and work function of the substrates show well-defined structure formation with an increase in fluence, similar to the trend obtained previously in the SEM analysis in Figure 3. KPFM is an atomic force microscope–based technique aiding in determining the changes in the work function and the surface potential in a nondestructive manner. In KPFM, the distributed contact potential difference ($V_C$) between the scanning tip and the sample is calculated as follows:

$V_C=e\left({\varphi }_{tip}-{\varphi }_{sample}\right),(2)$

where ${\varphi }_{tip}$ ($\sim$ 5.0 eV) and ${\varphi }_{sample}$ are the work functions of the tip and sample, respectively, while e is the electronic charge. The work function of the sample is calculated from the local potential change due to the presence of undulations on the surface. The local surface potential is averaged over a finite effective area of the surface involved in the interaction with the tip. In KPFM, the sample potential thus contributes to a bigger volume of the tip than its nanometric apex. Hence, an effective work function is calculated over the region where the stylus is scanning. Since the samples are irradiated uniformly, the overall work function has decreased. In the valley regions surrounding the microconical tips, the work function is observed to be 4.85 eV, while in the tip region, there is a significant decrease to 4.69 eV for fluence of 4.7 $\times$ 10¹⁸ cm⁻². For the pristine sample, the variation in work function is over a short range from 4.97 to 5.09 eV, which is because the pristine substrate has no implanted argon ions and more or less has uniform height distribution ($<$100 nm) as seen in Figure 4A.

FIGURE 4

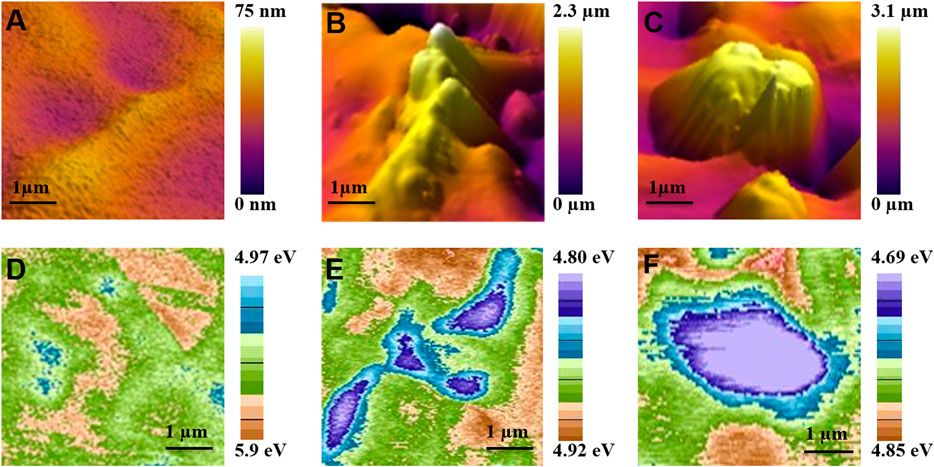
FIGURE 4. AFM topography (5 μm $\times$ 5 μm scan area) of (A) pristine Cu sheet, 2 keV Ar⁺ bombarded Cu sheet at normal incidence with fluence; (B) 3.2 $\times$ 10¹⁸ cm⁻² and (C) 4.7 $\times$ 10¹⁸ cm⁻². KPFM image showing the surface work function modification (D) pristine and corresponding Cu irradiated by Ar at fluence (E) 3.2 $\times$ 10¹⁸ cm⁻² and (F) 4.7 $\times$ 10¹⁸ cm⁻².

Figure 5A shows high resolution spectra of argon with peaks at Ar 2p_1/2 ($\sim$ 244.1 eV) and Ar 2p_3/2 ($\sim$ 241.8 eV) determined using XPS. A Shirley background fit is done to fit the XPS measurements. The Savitzky–Golay smoothing is done for multipeak analysis which is a standard smoothing procedure done to fit the XPS data. The peaks are resolved at $\text{Δ}$E = 2.3 eV, indicating inertness of Ar embedded on the metal surface. After argon irradiation, the intensities of the two peaks (Ar 2p_1/2 and Ar 2p_3/2) have increased, as seen from their areal coverage. For a flux of 4.7 $\times$ 10¹⁸ cm⁻² the argon concentration is the highest $\sim$ 3.89$\text{\%}$ and for 2.5 $\times$ 10¹⁸ cm⁻² the argon concentration is $\sim$ 2.72$\text{\%}$. The implantation depth of ions and their concentration can be varied by adjusting the ion beam parameters such as energy of ions, fluence, gas pressure, and wave power, including projectile target geometry. The results confirm argon ion implantation on irradiated copper surface by introducing atomic heterogeneity on the exposed surface and contributing significantly to the variation in the local work function. The pristine sample shows zero argon ion concentration from XPS analysis, which is consistent with the fact that the argon ions are not adsorbed on the exposed surface from environmental contamination, when exposed to external conditions while loading and unloading the samples. The XPS survey spectra are shown in Figure 5B. The as-prepared samples are preserved in a clean vacuum desiccator to avoid any exposure in the ambient air. The compositional studies revealed that an appreciable amount of oxygen and carbon is present in the near-surface atomic layers of the pristine and irradiated samples. Although the as-prepared samples are preserved in a clean vacuum desiccator to avoid any exposure in the ambient air, there could be some possibilities to absorb some atmospheric gases while transferring for measurements. The irradiated samples have a considerable amount of argon implanted whose percentage implantation is under our experimental control.

FIGURE 5

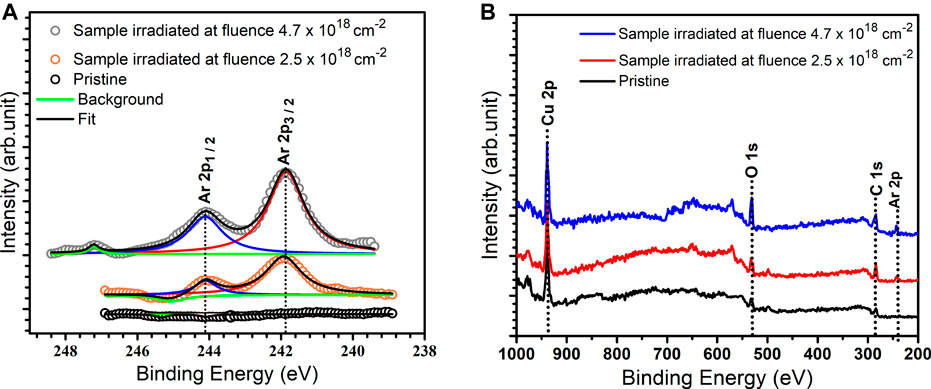
FIGURE 5. High-resolution X-ray photoelectron spectroscopy (XPS) spectra in (A) and X-ray photoelectron spectroscopy (XPS) survey spectra in (B) for two chosen argon-bombarded copper surface compared to pristine.

In Figure 6, the decrease in variation of work function distributed over the hillock (microconical tips) and valley (regions surrounding the microconical tips) regions, respectively, with the concentration of the implanted argon ions are plotted. The implanted argon concentration should increase with increase in time of exposure of the ion flux as the number of argon ions per unit area increases. The results obtained are consistent with this statement as they can be seen in Figures 5, 6. Argon implantation influence on the work function of metallic substrate is a comparatively new topic. A recent article aims at investigating the effect of particle irradiation on the work function in simple metals like Al and Zn using Ar⁺ ions at room temperature with 30 keV. The article uses similar KPFM technique and delves deep into understanding the theoretical aspects of the work function variation due to argon implantation [52].

FIGURE 6

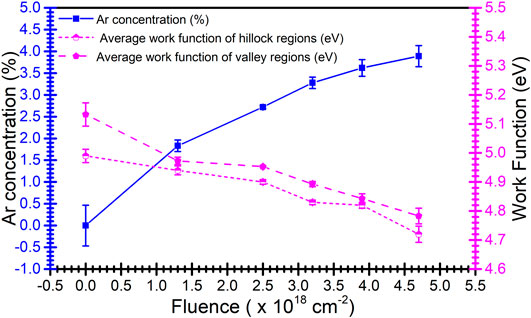
FIGURE 6. Variation of argon concentration (calculated from XPS data) and variation of the work function distributed over mounds (microhill regions) and relatively flat regions (obtained from KPFM data) with ion beam fluences.

The field emission experiment is performed using the micro conical structured substrates. The Fowler–Nordheim (FN) relation can be written in terms of the experimentally measured emission current (I) and applied voltage (V) as follows [53]:

$\text{ln}\left(\frac{I}{V^2}\right)=-\frac{Bd{\varphi }^{\frac{3}{2}}}{V\beta }+\text{ln}\left(\frac{AS{\beta }^2}{{\varphi }^{\frac{3}{2}}{d}^2}\right),(3)$

where ϕ is the bulk work function (4.99 eV), d is the gap distance, S is the effective area, and A and B are constants as defined earlier in Eq. 1.

The characteristics of emission current versus applied voltage plot are shown in Figure 7A and the corresponding FN plot in Figure 7B. It is evident from the experimental data tabulated in Table 1 that there is a decrease in the work function with an increase in fluence. This is observed due to the formation of the atomically heterogeneous surface with increased production of uniformly aligned distinct micro conical tips as seen in Figure 3. Thus, the emission of electrons from these irradiated surfaces at a higher fluence is easier at a comparatively low applied voltage (turn-on voltage), as seen in Figure 7A. The turn-on voltage for substrate irradiated with a fluence of 4.7 $\times$ 10¹⁸ cm⁻² is 2.33 kV, is significantly lower than that of the pristine sample having a turn-on voltage of 6.51 kV. The FN plot in Figure 7B is fitted with a straight line and the field enhancement factor (β) is extracted from the slope.

$\beta =-\frac{\left(6.8\times {10}^3\right){\varphi }^{\frac{3}{2}}d}{slope}.(4)$

FIGURE 7

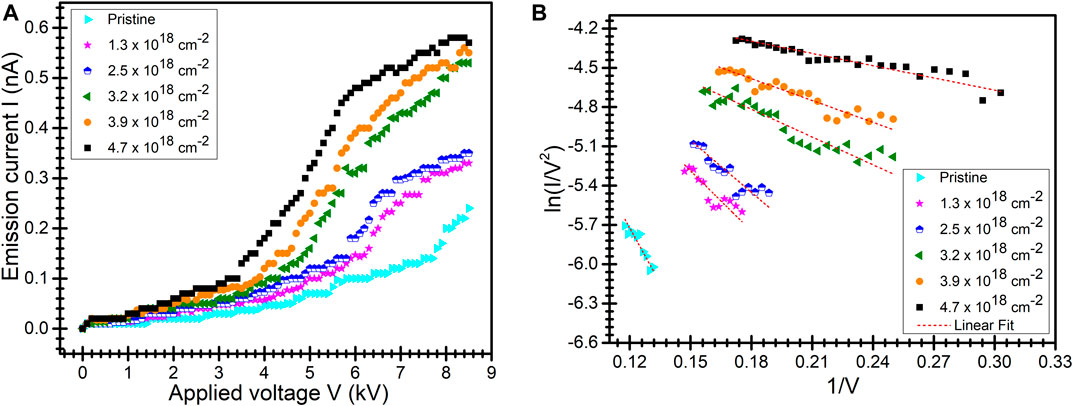
FIGURE 7. (A) Characteristics of field emission current (I) variation with the applied electric field (V) plot for individual fluences. (B) Fowler–Nordheim equation plot of pristine and irradiated Cu sheets by 2 keV argon ions beam. Voltage is measured in kilovoltage, while current is measured in nanoampere.

TABLE 1

TABLE 1. A comparison of implanted argon concentration, work function variation with microcones distribution for pristine and irradiated samples.

The field enhancement factor is a morphology- and work function–dependent parameter, affecting the local field around micro (nano)-scale protrusions on the metal surface. There is a significant rise in steepness of the linear fitting on experimentally observed curves (and consequently the enhancement factor), with an increase in fluence.

As previously stated, the Fowler–Nordheim equation assumes a smooth planar metal surface with a given work function. But the observed work function gets modified due to both protrusion formation and subsurface implantation of argon ions causing a considerable change in the field emission properties of any ion irradiated substrate. Thus, assuming the bulk work function of substrate in calculating the field emission parameters particularly for irradiated samples may produce erroneous results. To explain our experimental results on field emission, we consider a parametric model to describe the field emission properties for atomically heterogeneous surfaces where the work function is taken to vary across the area encompassing both hilly and valley regions, implanted impurities, and structural deformities. We consider the effective work function to be a linear combination of the work function observed over the undulated surfaces. The parameters γ and δ are the effective proportions in which hillocks and valley areas are distributed for a particular substrate observed using images obtained after analysis from KPFM and SEM results. Using ImageJ software, the hilly regions obtained in digital scan are demarcated and isolated. The areal percentage is calculated from the pixel density and then, incorporated in their corresponding color coded regions to obtain the percentage of work function and aspect ratio contributions. ImageJ software is well-known software used to isolate digital image of cells in soft matter to calculate their areal percentage using pixel density difference of the image taken [54]. The effective work function thus becomes ${\varphi }_{eff}$, and is given as follows:

${\varphi }_{eff}=\gamma {\varphi }_1+\delta {\varphi }_2,(5)$

which is employed in Eq. 3 in the place of ϕ and the β obtained is labeled as ${\beta }^{\text{*}}$ which is obtained directly from the slope as discussed earlier. ${\varphi }_1$ and ${\varphi }_2$ are area-averaged work functions of hilly and valley regions, respectively.

In Figure 8A, the work function variation of both hillock-like and valley regions with aspect ratio is shown. The aspect ratio decreases with the increase in fluence with the formation of prominent and well-defined hillocks and valleys. The valleys are basically upturned conics where there is significant contribution from the nonuniform side of the slopes. Thus, the work function decreases for both hilly and valley regions leading to the extraction of electrons with ease and increase in the enhancement factor. In Figure 8B, the enhancement factor is plotted along with the aspect ratio as a function of ion beam fluence. The electron emission from these structures with low aspect ratio is relatively easy because of their pointed geometry and small radius of curvature. The generation of naturally selected absolute uniform sets of sub-microconical metallic arrays having each tip of similar height and base diameter is difficult. Hence, we have calculated the average aspect ratio for each of the irradiated samples. The aspect ratio is defined as ratio of the base width of the conical structure and its corresponding height, averaged over a number of such microprotrusions evaluated from the SEM analysis. The aspect ratio is found to be in the range of 0.7–1.5, implying low aspect ratio for pointed microstructures. The electrons can easily tunnel through such configuration with additional aid from the local surface charge developed in the vicinity of such structures. The presence of implanted argon ions may also influence the surface charge production significantly by causing variation in the enhancement factor. The modified enhancement factor ${\beta }^{\text{*}}$ obtained by employing modified work function (${\varphi }_{eff}$) is compared with enhancement factor β and evaluated considering bulk work function ϕ in Table 2. The overall high values of the enhancement factor are due to the increase of the field emission current due to atomic-level surface defects such as implantation of atoms and locally attached surface adatoms apart from the sharp surface deformities. It may be understood that the change occurring at the valley regions is just because of the subsurface argon atoms which perhaps modify the density of states and lead to a lowering of the work function. The change happening at the hilly regions (conical tips) is a combination of the effect of the implanted argon impurities and the field enhancement. These contributions are not accounted for in the original Fowler–Nordheim equations. Moreover, vacuum electronics are sensitive to micro- and nanometric deformities. Hence, more precise evaluation of the enhancement factor is beneficial over the enhancement factor which has already been evaluated purely considering the bulk work function. Thus, the parametric modeling focuses on the need for considering individual topographical contribution of ion-irradiated surfaces as these micrometric surface effects infact influence the effectivity of field emitters.

FIGURE 8

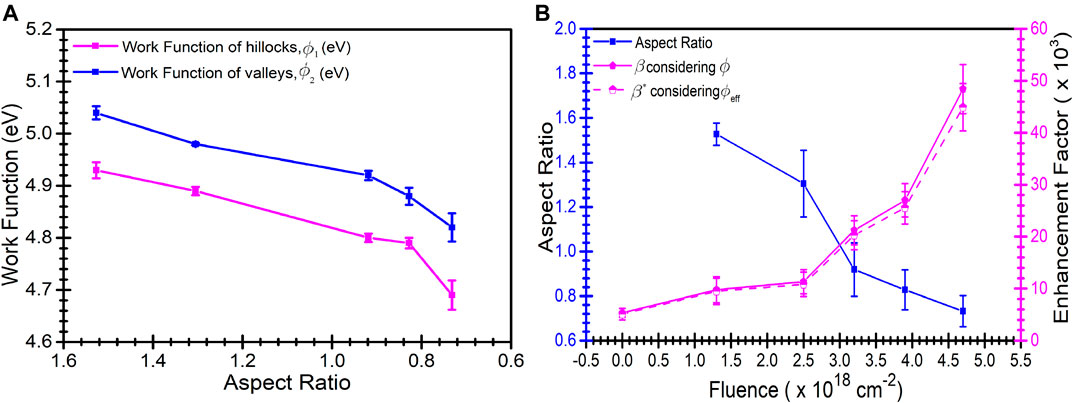
FIGURE 8. (A) Work function of both hillocks and valleys variation with aspect ratio. (B) Variation of aspect ratio and field enhancement factor (β and ${\beta }^{\text{*}}$) calculated from both bulk (ϕ) and modified work function (${\varphi }_{eff}$) with beam fluence.

TABLE 2

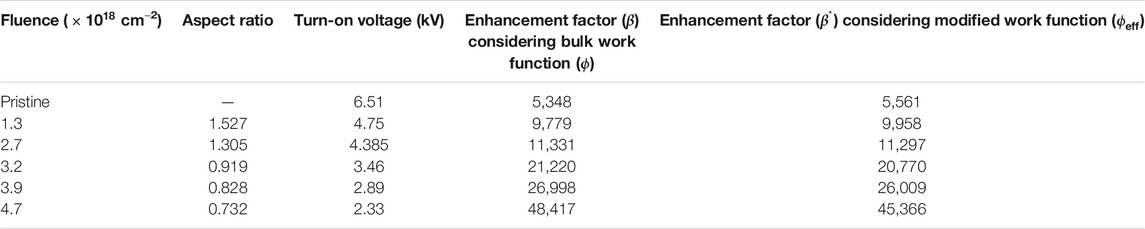
TABLE 2. A comparison of aspect ratio of structures with turn on voltage and enhancement factor obtained considering bulk and modified work function, for pristine and irradiated samples.

5 Summary

In conclusion, the present study revisits sputter cones like structure with well-defined arrays of conical hillocks of micrometer dimension, challenging their requirements for seeded impurity atoms along with exploring their possibilities as promising field emitters. The growth mechanism of microconical arrays needs to be explored with a proper support from the substrate-oriented and modified existing theories in a channelized manner. The high enhancement factor of pristine is due to copper being a highly conductive metal, but the subsequent increase in the enhancement factor with field emission current for irradiated surfaces is because of the formation of atomically heterogeneous system (by low energy plasma ion irradiation) with multiple microprotrusions. The field emission results have shown almost eight times increase in the field enhancement factor for high fluence irradiation (4.7 $\times$ 10¹⁸ cm⁻²). The local variation of work function is mainly due to the evolution of the structural deformities and implantation of argon ions as observed from the employed experimental techniques and reported in this article. In our parametric model, we have tried to tune the effects of the work function of modified atomically heterogeneous surface on their field emission parameters. From the results presented so far, we could satisfy the objective of presenting these newly formed naturally selected structures and side by side show the need for modified Fowler–Nordheim theory as a slight change in the work function brought about by the deformed atomically heterogeneous system produces significant change in the experimentally obtained field emission parameters.

Hence, there is a requirement for a relook at the existing FN theory for incorporating the effects of both the work function variation due to atomically heterogeneous surface and the corresponding field enhancement at the microconical tips. As a future work, it would be helpful to distinguish between the contribution of surface structure formation and heterogeneity introduction separately on the increase in field emission parameters. Experimental techniques aimed at masking the geometric effects of micro protrusions on field enhancement factor so that the effect of atomically heterogeneous surface layer influencing the field emission parameters that is discernible may be devised. A theoretical model based on understanding of the individual contribution of the parameters obtained from the experimental results and analysis, where a statistical distribution of arrays of microconics may be considered on a pure copper substrate. These microconical arrays with randomly distributed implanted inert gas ions will then represent the irradiated substrate for a comparative study with the experimentally obtained results.

Data Availability Statement

The original contributions presented in the study are included in the article, and further inquiries can be directed to the corresponding authors.

Author Contributions

JM and SB: designed and carried out the experiments, analyzed the experimental results, and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

JM and SB gratefully acknowledge Mr. Omprakash and his colleagues of Physics workshop, IIT Kanpur for helping with the design and fabrication. We acknowledge fruitful discussions with Prof. John H. Booske, UW-Madison, United States. We thank Prof. Ashish Garg, for the AFM and KPFM measurements, the Centre of Nanosciences, for the SEM measurements and the Advanced Center for Materials Science (ACMS) for the XPS measurements (IIT Kanpur). JM thanks Dr. Dipak Bhowmik for introducing the Casa XPS software.

References

1. Heinig KH, Müller T, Schmidt B, Strobel M, Müller W. Interfaces under Ion Irradiation: Growth and Taming of Nanostructures. Appl Phys A: Mater Sci Process (2003) 77:17–25. doi:10.1007/s00339-002-2061-9

CrossRef Full Text | Google Scholar

2. Chan WL, Chason E. Making Waves: Kinetic Processes Controlling Surface Evolution during Low Energy Ion Sputtering. J Appl Phys (2007) 101:121301. doi:10.1063/1.2749198

CrossRef Full Text | Google Scholar

3. Albrecht M, Christiansen S, Michler J, Dorsch W, Strunk HP, Hansson PO, et al. Surface Ripples, Crosshatch Pattern, and Dislocation Formation: Cooperating Mechanisms in Lattice Mismatch Relaxation. Appl Phys Lett (1995) 67:1232–4. doi:10.1063/1.115017

CrossRef Full Text | Google Scholar

4. Kajita S, Yoshida T, Kitaoka D, Etoh R, Yajima M, Ohno N, et al. Helium Plasma Implantation on Metals: Nanostructure Formation and Visible-Light Photocatalytic Response. J Appl Phys (2013) 113:134301. doi:10.1063/1.4798597

CrossRef Full Text | Google Scholar

5. Zhu J-h., Brunner K, Abstreiter G. Two-dimensional Ordering of Self-Assembled Ge Islands on Vicinal Si(001) Surfaces with Regular Ripples. Appl Phys Lett (1998) 73:620–2. doi:10.1063/1.121875

CrossRef Full Text | Google Scholar

6. Chang T, Kunuku S, Sankaran KJ, Leou K-C, Tai N, Lin I-N. Enhancing the Stability of Microplasma Device Utilizing diamond Coated Carbon Nanotubes as Cathode Materials. Appl Phys Lett (2014) 104:223106. doi:10.1063/1.4881419

CrossRef Full Text | Google Scholar

7. Liu J, Zeng B, Wu Z, Zhu J, Liu X. Improved Field Emission Property of Graphene Paper by Plasma Treatment. Appl Phys Lett (2010) 97:033109. doi:10.1063/1.3467042

CrossRef Full Text | Google Scholar

8. Lam S-T. Overview of Field-Emission Information Storage Devices. J Vac Sci Technol B (2003) 21:479–82. doi:10.1116/1.1541603

CrossRef Full Text | Google Scholar

9. Egorov N, Sheshin E. Field Emission Electronics. Cham: Springer (2017). doi:10.1007/978-3-319-56561-3

CrossRef Full Text

10. Kuznetzov AA, Lee SB, Zhang M, Baughman RH, Zakhidov AA. Electron Field Emission from Transparent Multiwalled Carbon Nanotube Sheets for Inverted Field Emission Displays. Carbon (2010) 48:41–6. doi:10.1016/j.carbon.2009.08.009

CrossRef Full Text | Google Scholar

11. Jin F, Beaver A. High Thermionic Emission from Barium Strontium Oxide Functionalized Carbon Nanotubes Thin Film Surface. Appl Phys Lett (2017) 110:213109. doi:10.1063/1.4984216

CrossRef Full Text | Google Scholar

12. Han JS, Bredow T, Davey DE, Yu AB, Mulcahy DE. The Effect of Al Addition on the Gas Sensing Properties of Fe₂O₃-Based Sensors. Sensors Actuators B: Chem (2001) 75:18–23. doi:10.1016/S0925-4005(00)00688-2

CrossRef Full Text | Google Scholar

13. Xu CX, Sun XW, Chen BJ. Field Emission from Gallium-Doped Zinc Oxide Nanofiber Array. Appl Phys Lett (2004) 84:1540–2. doi:10.1063/1.1651328

CrossRef Full Text | Google Scholar

14. Gohel A, Chin KC, Zhu YW, Sow CH, Wee ATS. Field Emission Properties of N₂ and Ar Plasma-Treated Multi-wall Carbon Nanotubes. Carbon (2005) 43:2530–5. doi:10.1016/j.carbon.2005.05.003

CrossRef Full Text | Google Scholar

15. Tsai W-C, Wang S-J, Chang C-L, Chen C-H, Ko R-M, Liou B-W. Improvement of Field Emission Characteristics of Tungsten Oxide Nanowires by Hydrogen Plasma Treatment. Europhys Lett (2008) 84:16001. doi:10.1209/0295-5075/84/16001

CrossRef Full Text | Google Scholar

16. Tanyeli İ, Marot L, van de Sanden MCM, De Temmerman G. Nanostructuring of Iron Surfaces by Low-Energy Helium Ions. ACS Appl Mater Inter (2014) 6:3462–8. doi:10.1021/am405624v

CrossRef Full Text | Google Scholar

17. Zhang K, Bobes O, Hofsäss H. Designing self-organized nanopatterns on si by ion irradiation and metal co-deposition. Nanotechnology (2014) 25:085301. doi:10.1088/0957-4484/25/8/085301

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kim TC, Ghim C-M, Kim HJ, Kim DH, Noh DY, Kim ND, et al. Kinetic Roughening of Ion-Sputtered Pd(001) Surface: Beyond the Kuramoto-Sivashinsky Model. Phys Rev Lett (2004) 92:246104. doi:10.1103/PhysRevLett.92.246104

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ozaydin G, Özcan AS, Wang Y, Ludwig KF, Zhou H, Headrick RL, et al. Real-time x-ray studies of Mo -seeded Si nanodot formation during ion bombardment. Appl Phys Lett (2005) 87:163104. doi:10.1063/1.2099521

CrossRef Full Text | Google Scholar

20. McCracken GM. A Review of the Experimental Evidence for Arcing and Sputtering in Tokamaks. J Nucl Mater (1980) 93-94:3–16. doi:10.1016/0022-3115(80)90299-8

CrossRef Full Text | Google Scholar

21. You JB, Zhang XW, Cai PF, Dong JJ, Gao Y, Yin ZG, et al. Enhancement of Field Emission of the Zno Film by the Reduced Work Function and the Increased Conductivity via Hydrogen Plasma Treatment. Appl Phys Lett (2009) 94:262105. doi:10.1063/1.3167301

CrossRef Full Text | Google Scholar

22. Zheng Z, Liao L, Yan B, Zhang JX, Gong H, Shen ZX, et al. Enhanced Field Emission from Argon Plasma-Treated Ultra-sharp α-Fe₂O₃ Nanoflakes. Nanoscale Res Lett (2009) 4:1115–9. doi:10.1007/s11671-009-9363-1

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chatterjee S, Bhattacharjee S, Maurya SK, Srinivasan V, Khare K, Khandekar S. Surface Wettability of an Atomically Heterogeneous System and the Resulting Intermolecular Forces. Europhys. Lett. (2017) 118:68006. doi:10.1209/0295-5075/118/68006

CrossRef Full Text | Google Scholar

24. Chowdhury A, Bhattacharjee S. Localized Subsurface Modification of Materials Using Micro-low-energy Multiple Ion Beamlets. AIP Adv (2011) 1:042150. doi:10.1063/1.3664753

CrossRef Full Text | Google Scholar

25. Singh KP, Majumdar J, Bhattacharjee S. Tuning Optical Properties of Atomically Heterogeneous Systems Created by Plasma-Based Low-Energy Ion Beams. Appl Opt (2020) 59:4507–16. doi:10.1364/AO.390751

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Ritter M, Stindtmann M, Farle M, Baberschke K. Nanostructuring of the Cu(001) Surface by Ion Bombardment: a STM Study. Surf Sci (1996) 348:243–52. doi:10.1016/0039-6028(95)01024-6

CrossRef Full Text | Google Scholar

27. Feng L, Yan H, Li H, Zhang R, Li Z, Chi R, et al. Excellent Field Emission Properties of Vertically Oriented Cuo Nanowire Films. AIP Adv (2018) 8:045109. doi:10.1063/1.5022320

CrossRef Full Text | Google Scholar

28. Evangelakis GA, Papanicolaou NI. Adatom Self-Diffusion Processes on (001) Copper Surface by Molecular Dynamics. Surf Sci (1996) 347:376–86. doi:10.1016/0039-6028(95)00991-4

CrossRef Full Text | Google Scholar

29. Zhu YW, Moo AM, Yu T, Xu XJ, Gao XY, Liu YJ, et al. Enhanced Field Emission from O₂ and CF₄ Plasma-Treated Cuo Nanowires. Chem Phys Lett (2006) 419:458–63. doi:10.1016/j.cplett.2005.11.087

CrossRef Full Text | Google Scholar

30. Schäfer C, Gollmer DA, Horrer A, Fulmes J, Weber-Bargioni A, Cabrini S, et al. A Single Particle Plasmon Resonance Study of 3d Conical Nanoantennas. Nanoscale (2013) 5:7861–6. doi:10.1039/C3NR01292A

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Camarero J, Cros V, Capitán MJ, Álvarez J, Ferrer S, Niño MA, et al. Epitaxial Growth of Metals with High Ehrlich-Schwoebel Barriers and the Effect of Surfactants. Appl Phys A: Mater Sci Process (1999) 69:553–7. doi:10.1007/s003390051469

CrossRef Full Text | Google Scholar

32. Martynenko YV, Nagel’ MY. Model of Fuzz Formation on a Tungsten Surface. Plasma Phys Rep (2012) 38:996–9. doi:10.1134/S1063780X12110074

CrossRef Full Text | Google Scholar

33. Bradley RM, Harper JME. Theory of Ripple Topography Induced by Ion Bombardment. J Vacuum Sci Technology A: Vacuum, Surf Films (1988) 6:2390–5. doi:10.1116/1.575561

CrossRef Full Text | Google Scholar

34. Cuerno R, Barabási A-L. Dynamic Scaling of Ion-Sputtered Surfaces. Phys Rev Lett (1995) 74:4746–9. doi:10.1103/PhysRevLett.74.4746

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wehner GK, Hajicek DJ. Cone Formation on Metal Targets during Sputtering. J Appl Phys (1971) 42:1145–9. doi:10.1063/1.1660158

CrossRef Full Text | Google Scholar

36. Wehner GK. Cone Formation as a Result of Whisker Growth on Ion Bombarded Metal Surfaces. J Vacuum Sci Technology A: Vacuum, Surf Films (1985) 3:1821–35. doi:10.1116/1.573386

CrossRef Full Text | Google Scholar

37. Robinson RS, Rossnagel SM. Ion‐beam‐induced Topography and Surface Diffusion. J Vacuum Sci Technology (1982) 21:790–7. doi:10.1116/1.571826

CrossRef Full Text | Google Scholar

38. Davidovitch B, Aziz MJ, Brenner MP. On the Stabilization of Ion Sputtered Surfaces. Phys Rev B (2007) 76:205420. doi:10.1103/PhysRevB.76.205420

CrossRef Full Text | Google Scholar

39. Bradley RM. Theory of Nanodot and Sputter Cone Arrays Produced by Ion Sputtering with Concurrent Deposition of Impurities. Phys Rev B (2011) 83:195410. doi:10.1103/PhysRevB.83.195410

CrossRef Full Text | Google Scholar

40. Perkinson JC, Anzenberg E, Aziz MJ, Ludwig KF. Model-independent Test of the Truncated Crater Function Theory of Surface Morphology Evolution during Ion Bombardment. Phys Rev B (2014) 89:115433. doi:10.1103/PhysRevB.89.115433

CrossRef Full Text | Google Scholar

41. Fowler RH, Nordheim L. Electron Emission in Intense Electric fields. Proc R Soc Lond Ser A, Containing Pap a Math Phys Character (1928) 119:173–81. doi:10.1098/rspa.1928.0091

CrossRef Full Text | Google Scholar

42. Kajita S, Ohno N, Hirahata Y, Hiramatsu M. Field Emission Property of Nanostructured Tungsten Formed by Helium Plasma Irradiation. Fusion Eng Des (2013) 88:2842–7. doi:10.1016/j.fusengdes.2013.05.014

CrossRef Full Text | Google Scholar

43. Kyritsakis A, Xanthakis JP. Derivation of a Generalized Fowler-Nordheim Equation for Nanoscopic Field-Emitters. Proc R Soc A (2015) 471:20140811. doi:10.1098/rspa.2014.0811

CrossRef Full Text | Google Scholar

44. Biswas D, Ramachandran R. Curvature Correction to the Field Emission Current. J Vacuum Sci Technology B (2019) 37:021801. doi:10.1116/1.5064403

CrossRef Full Text | Google Scholar

45. Kildemo M, Calatroni S, Taborelli M. Breakdown and Field Emission Conditioning of Cu, Mo, and W. Phys Rev ST Accel Beams (2004) 7:092003. doi:10.1103/PhysRevSTAB.7.092003

CrossRef Full Text | Google Scholar

46. Djurabekova F, Ruzibaev A, Holmström E, Parviainen S, Hakala M. Local Changes of Work Function Near Rough Features on Cu Surfaces Operated under High External Electric Field. J Appl Phys (2013) 114:243302. doi:10.1063/1.4856875

CrossRef Full Text | Google Scholar

47. Toijala H, Eimre K, Kyritsakis A, Zadin V, Djurabekova F. Ab Initio calculation of Field Emission from Metal Surfaces with Atomic-Scale Defects. Phys Rev B (2019) 100:165421. doi:10.1103/PhysRevB.100.165421

CrossRef Full Text | Google Scholar

48. Chowdhury A, Chatterjee S, Dutta A, Bhattacharjee S. Stopping Potential and Ion Beamlet Control for Micro-resistive Patterning through Sub-debye Length Plasma Apertures. AIP Adv (2014) 4:127127. doi:10.1063/1.4904371

CrossRef Full Text | Google Scholar

49. Chowdhury A, Bhattacharjee S. Micron-focused Ion Beamlets. J Appl Phys (2010) 107:093307. doi:10.1063/1.3371688

CrossRef Full Text | Google Scholar

50. Maurya SK, Barman S, Paul S, Bhattacharjee S. Charge Dissipation and Self Focusing Limit in High Current Density Ion Beam Transport through a Micro Glass Capillary. J Phys D: Appl Phys (2018) 52:055205. doi:10.1088/1361-6463/aaef4b

CrossRef Full Text | Google Scholar

51. Frost F, Fechner R, Ziberi B, Völlner J, Flamm D, Schindler A. Large Area Smoothing of Surfaces by Ion Bombardment: Fundamentals and Applications. J Phys Condens Matter (2009) 21:224026. doi:10.1088/0953-8984/21/22/224026

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Horváth Á, Nagy N, Vértesy G, Schiller R. Phenomenology of the Effect of Ion Irradiation on the Work Function of Metals. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms 466 (2020) 12–6. doi:10.1016/j.nimb.2020.01.004

CrossRef Full Text | Google Scholar

53. Bhattacharjee S, Vartak A, Mukherjee V. Experimental Study of Space-Charge-Limited Flows in a Nanogap. Appl Phys Lett (2008) 92:191503. doi:10.1063/1.2928232

CrossRef Full Text | Google Scholar

54. Schindelin J, Rueden CT, Hiner MC, Eliceiri KW. The Imagej Ecosystem: An Open Platform for Biomedical Image Analysis. Mol Reprod Dev (2015) 82:518–29. doi:10.1002/mrd.22489

PubMed Abstract | CrossRef Full Text | Google Scholar